Whole numbers are positive counting numbers. Whole numbers do not have any decimals and they cannot be fractions. The whole numbers are {0,1,2,3,4,5,...}

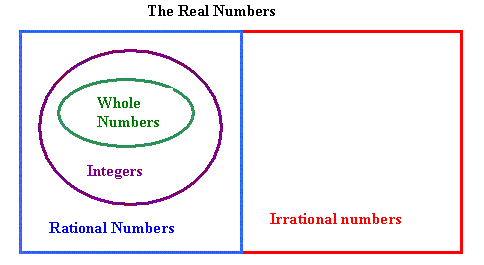Integers are the positive and negative counting numbers. Integers do not contain decimals and they cannot be fractions {Whole numbers} Ì {Integers} The Integers are {...-5,-4,-3,-2,-1,0,1,2,3,4,5,...}

Rational numbers are any number that can be expressed as a ratio of two integers (a ratio being one number placed over another with a "/" in between-we will examine this more thoroughly in the unit on fractions) {integers} Ì {Rational numbers} The Rational numbers include decimals, and fractions. Just as an example of some Rational numbers, {1/3, 5/1 (=5), -2/3, -2/1 (=-2), 0.56, -0.02} Ì {Rational numbers}

The Irrational numbers are any number that cannot be expressed as a ratio of two integers The greek constant pi, (p) which is used in calculating the area and curcumference of a circle, is one example of an Irrational number. p is approximately equal to 3.14 When you come to square roots later in this tutorial, you'll see other Irrational numbers

The Real numbers encompass everything {Real numbers}={Rational numbers} È {Irrational numbers}.

I know this isn't the most exciting subject but believe it or not these properties are how subjects like algebra work. Just drink a cup of coffee to stay awake, and it will be over in a minute

• COMMUTATIVE
  • The commutative property allows you to perform addition operations and multiplication operations in any order you wish.
    So the commutative property permits a + b = b + a and a x b = b x a.
    One example of this is: 3 + 4 = 4 + 3 and 3 x 4 = 4 x 3.
• ASSOCIATIVE
  • When performing addition or multiplication on three numbers, the associative property allows you to group them together in any order you wish.
    So (a + b) + c = a + (b + c) and (a x b) x c = a x (b x c).
    One example of this is: (2 + 3) + 4 = 2 + (3 + 4) and (2 x 3) x 4 = 2 x (3 x 4).
• DISTRIBUTIVE
  • This one involves addition and multiplication operations being performed together.
    It says that a x (b + c) = (a x b) + (a x c)
    One example of this is: 2 x (3 + 4) = (2 x 3) + (2 x 4)
• IDENTITY
  • the numbers 0 and 1 play an important role in math, since they do absolutely nothing.
    • Any number plus 0 equals itself.
      a + 0 = 0 + a = a.
      One example of this is: 3 + 0 = 0 + 3 = 3.
      0 is called the identity for addition.
    • Any number multiplied by 1 is equal to itself.
      a x 1 = 1 x a = a.
      One example of this is: 3 x 1 = 1 x 3 = 3
      1 is called the identity for multiplication.