|
|
23 means 2 multiplied by itself three times
So 2*2*2*7 could be written as 23*7
In 23 two (the number that you are multplying) is called the base
and three is called the exponent or power.
If we had an expression such as 3*3*3*3*3 that could be written as 35
The base 3 is being raised to the exponent 5 (or one could also say 3 raised to the 5th power)
meaning that 3 is being multiplied by itself 5 times.
If we had an expression 3*3*3*5*5*5*5, you could notice that 3 is multiplied by itself 3 times
and 5 is multiplied by itself 4 times so
3*3*3*5*5*5*5 = 33*54
[Note:Frequently the "*" is dropped, and this expression appears as 3354]
Now that you can write exponent notation let's see you decipher one
33*52 = ?
33*52 = (3*3*3) * (5*5) = 27 * 25 = 625.
Now I'll finish this section by exploring some special exponents
Anything raised to the exponent 1 equals itself.
21=2;
31=3;
41=4;
Anything raised to the exponent 0 is equal to one
30 = 1 ;
40 = 1 ;
50 = 1
The exponent 2 is used so often, it is given a special name: square or squared
2 square = 22 = 2*2= 4 ;
3 squared = 32 = 3*3= 9;
4 square = 42 = 4*4= 16
The exponent 3 is used so often that it is given a special name: cube or cubed
2 cubed = 23 = 2*2*2= 8;
3 cube = 33 = 3*3*3= 27;
4 cube = 43 = 4*4*4= 64
Our number system revolves around the number 10.
We basically only have nine digits 0 through 9, that we permutate to
form all of the other numbers.
For example the number 98,631 is just a combination of "9", "8", "6", "3" and "1."
But how we right those five digits makes all the difference.
13,689 uses the same five digits, but 13,689 is certainly not the same as 98,631.
Let's break our numbers down by the column that they appear in.
Starting on the left, the first digit in the "ones" column.
The next column is the "tens" column.
The next column is the "hundreds column and so on.
Each successive column goes up by a unit of ten.
The fourth column would be "thousands" ; the fifth "ten thousands" ; the sixth "hundred thousands"
What do you think the seventh column would be?
Using this pattern let's look at our numbers 98,631 and 13,689 again
98,631=1+30+600+8,000+90,000 or we could say
98,631 would be 1-"one" plus 3-"tens" plus 6-"hundreds" plus 8-"thousands" plus 9-"ten thousands"
Similarly
13,689=9+80+600+3,000+10,000 or we coul say
13,689 would be 9-"one" plus 8-"tens" plus 6-"hundreds" plus 3-"thousands" plus 1-"ten thousands"
Now you might think "That's very intersting, but what does it have to do with exponents?"
(or more likely you might yawn and say "that's very tranqualizing, but what does it have to do with exponents?)
Okay, let's look at the power's of ten
Now let's go back to out two numbers (bear with me, we're almost finished)
98,631=
90,000 = 9 * 10,000 = 9 * 104
+
8,000 = 8 * 1,000 = 8 * 103
+
600 = 6 * 100 = 6 * 102
+
30 = 3 * 10 = 3 * 101
+
1 = 1 * 1 = 1 * 100
98,631 = (9 * 104) + (8 * 103) + (6 * 102) + (3 * 101) + (1 * 100).
13,689 =
10,000 = 1 * 10,000 = 1 * 104
+
3,000 = 3 * 1,000 = 3 * 103
+
600 = 6 * 100 = 6 * 102
+
80 = 8 * 10 = 8 * 101
+
9 = 9 * 1 = 9 * 100
13,689 = (1 * 104) + (3 * 103) + (6 * 102) + (8 * 101) + (9 * 100).
What we just did is known as the base-10 representation of a number
Now if we can go forward, we must also be able to go backward, right?
Let's look at
(3*106)+(7*105) + (4*104) + (0*103) +
(2*102) + (1*101) + (7*100)
Disgusting, isn't it? But let's take it one step at a time
(3*106) = 3 * 1,000,000 = 3,000,000
(7*105) = 7 * 100,000 = 700,000
(4*104) = 4 * 10,000 = 40,000
(0*103) = 0 * 1,000 = 0
(2*102) = 2 * 100 = 200
(1*101) = 1 * 10 = 10
(7*100) = 7 * 1 = 7
Adding everything up we have 3,740,217.
One more point then your own your own.
Assuming, your still awake, you might ask "Who cares about all this mumbo-jumbo?"
Well, there are a few uses for this mumbo-jumbo. Here I'll mention two of them
If you ever wanted to study how computers operate, you would discover that
computers think of everything in binary or base-2
Furthermore, a knowledge of base 10 would be helpful in learning other bases such as binary.
An off-shoot of base-10 representation is scientific notation
Scientists frequently use scientific-notation when writing very large numbers.
For example the speed of light is approximately 186,000 miles per second.
This could be written as 186 * 103 (or more officially as 1.86 * 105
meaning move the decimal 5 places to the right, adding more zeros to the right of the 6)
Even more to the point is the mass of the Earth.
The mass of the earth is approximately 1317 * 1022 lbs.
Imagine writing 22 zeros behind the 7 in 1317.
(The scientific notation would be officially written as 1.317 * 1025 lbs.
meaning move the decimal 25 places to the right, adding more zeros to the right of the 7)
Square roots are generally designated by a symbol that looks a little like the division symbol with a "v" attached to it
=b means the same thing as saying b2=a
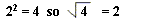
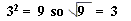
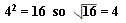
Not all square roots come out so nicely.
In fact, the ones that do come out to be whole numbers, like 4, 9, and 16, are called perfect squares
Perfect squares are squares of whole numbers.
Other perfect squares include 25, 100, 121, and 144.
As I mentioned above not all square roots turn out to be whole numbers.
For example 
not only is
not a whole number, but it turns out to be an irrational number (An irration number is one which
cannot be expressed as a ratio or a fraction of two whole numbers).
We can however approximate the value of .
is approximately equal to 1.414.
You can use a calculator just this once to verify this statement.
Now put it in a drawer, lock it up, and pretend that the calculator does not exist.
Other square roots that turn out to be irrational include 
I have a question for you:
Does the square root of a sum equal the sum of the square roots?
In other words does
?
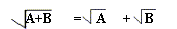The actual answer of the above question is "no."
(Don't feel bad if you thought the answer was "yes." I did too when I was learning this stuff, as did several other people.)
To disprove a statement, all that has to be done is giving one example where the statement turns out to be false.
I'll be doing that right now.
Consider the number 25.
25 = 16 + 9
So the above statement could be written as:
does
?
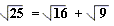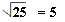
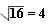
Thus 
= 4 + 3 = 7
and 5 is certainly not equal to 7.
One last question: Does the square root of a product equal the product of the square roots.
In other words does 
?
After the last question, you might think the answer is "no", but in this case the answer is "yes."
Okay, how does that help us?
Well, what if we can factor the original number and one of the factors is a perfect square.
Then we can reduce our square root.
Look at the next two examples, to see what I am refering to.
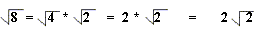
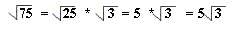
Notice how the "*" is dropped in the last step leaving just the whole number, and the square root.