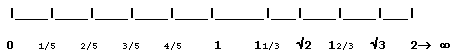0 1 2 3 4 5 ® ¥
Now if we magnified the section between 0 and 2 we would see the following:
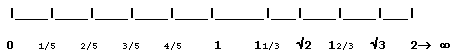
Remember that Ö2 and Ö3 are
irrational numbers whose approximate values are 1.414 and 1.732 respectively.
So there you have it. a graphic display of whole numbers, positive rational numbers, and positve irrational numbers.
Coming up next: We'll complete the real number system by extending the number line to the left to include negative numbers.
INTRODUCTION TO NEGATIVE NUMBERS
Negative numbers look just like the numbers you are used to, except there is a "-" in front of them.
Negative numbers include -1, -Ö2 (which would apprximately equal -1.414), -2, and -3 1/4
They represent numbers that are actually less than zero, and comprise the left side of a number line.
One way that I have found helps some people understand negative numbers is to think about money.
Think of
a positive number as money that you have,
and a negative number as money that you owe.
Below you'll see a number line going from -5 to 5.
[Note to the reader: we could write 5 as "+5" to emphasize the fact that it is a positive number,
but it really is not necessary. A number without a sign ("+" or "-") in front of it is always assumed to be positive]
|___|___|___|___|___|___|___|___|___|___|
-¥ ¬ -5 -4 -3 -2 -1 0 1 2 3 4 5 ® ¥
Notice the negative side stretches on to -¥, and goes in the
opposite direction as compared to positve numbers
(-5 is to the left of -4, which in turn is to the left of -3, etc.)
In general when number lines are drawn, you see the arrow(s), but the infinity sign(s) are omitted.
From here on out that is how I will draw number lines. The infinity sign(s) will just be assumed.
COMPARING NUMBERS
First of all, we have to bring < and > out of retirement.
a < b means a is less than b (example: 3 < 4)
a > b means a is greater than b (example: 4 > 3)
Now we're almost ready to compare numbers, both positive and negative.
|___|___|___|___|___|___|___|___|___|___|
¬ -5 -4 -3 -2 -1 0 1 2 3 4 5 ®
The most important thing to remember is the number line is always read from left to right.
So even though it may not look like it, -5 < 3 since -5 is to the left of 3.
If it helps you to consider positive and negative numbers in a monetary sense,
owing $5 (-5) is certainly less desirable than having $3
However, if we were going to compare -3 and -5,
-3 > -5 since -3 is to the right of -5.
If it helps you to consider positive and negative numbers in a monetary sense,
owing $3 (-3) is certainly better than owing $5 (-5)
In each of the following exercises place "<" or ">" in the text box
Exercise 1
Go to the next problem
Go to the top of this page
Go to the Number line/Negative numbers main page
Go to the next section
Exercise 2
Go to the next problem
Go to the top of this page
Go to the Number line/Negative numbers main page
Go to the next section
Exercise 3
Go to the next problem
Go to the top of this page
Go to the Number line/Negative numbers main page
Go to the next section
Exercise 4
Go to the next problem
Go to the top of this page
Go to the Number line/Negative numbers main page
Go to the next section
Exercise 5
Go to the top of this page
Go to the Number line/Negative numbers main page
Go to the next section