UNION, INTERSECTION, AND SUBSETS
UNION
Has the following set of events ever occurred to you while shopping.
You go into one store and see several items you would like to buy, and
then you go into another store and see more items you would like to buy.
You simply can't decide which object to purchase, you want it all!
In "math talk" what you just experienced is a union.
A union of two or more sets is another set that contains everything
contained in the previous sets.
Union is designated by the symbol È.
If A and B are sets then A È B represents the union of A and B
In the examples below you'll see the union of sets, then
it will be time for you to put together some sets of your own.
Example 1
A={1,2,3,4,5} B={5,7,9,11,13}
A È B = {1,2,3,4,5,7,9,11,13}
Notice that when I wrote out the united set I did not write "5" twice.
I simply listed all of the new sets elements.
Example 2
A={all the books written by Charles Dickens}
B={all the books written by Mark Twain}
A È B = {all books written by either Charles Dickens or Mark Twain}
In each of the following examples construct the union of the two sets.
Place your answer in the text box and then click on "check my answer"
While writing your answer please remember:
- In order for the computer to check your answer the entries must be in numerical
(or alphabetical) order.
This is generally not true for sets.
- Place commas between the elements
- Your answer should start with a "{" and end with a "}"
Exercise 1
A={1,2,3} B={6,7,8}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 2
A={2,4,6,8} B={1,2,3,4,5}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 3
A={a,e,i,o,u} B={h,i,j,k,l}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 4
A={a,b,c} B={a,b,c,d,e}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 5
A={1,2,3,4} B={3,4,11,22}
Go to the top of this page
Go to the set home page
Go to the next section
INTERSECTION
Let's go back to our stores for a moment.
Have you ever noticed two
or more stores that carry the same merchandise?
What you observed is an example of intersection.
The intersection of two (or more) sets is those elements that they have in common.
Intersection is designated by the symbol Ç.
So if A and B are sets then the intersection (the elements they both have in common) is donated by A Ç B.
In the following examples you will have a chance to see intersection in action.
Example 1
A={1,3,5,7,9} B={2,3,4,5,6}
The elements they have in common are 3 and 5
A Ç B = {3,5}
Example 2
A={The English alphabet} B={vowels}
So A Ç B = {vowels}
Example 3
A={1,2,3,4,5} B={6,7,8,9,10}
In this case A and B have nothing in common.
As usual, we have a symbol for this phenomenon: {Æ}.
{Æ} is called the “empty set.”
A Ç B = {Æ}
(See back on page 1 of this unit, I told you that there would be a set with nothing in it)
Well that’s all I have to write about intersection, at least for now. So it’s time for you to get your chance.
In each of the following examples construct the intersection of the two sets.
Place your answer in the text box and then click on "check my answer"
While writing your answer please remember:
- In order for the computer to check your answer the entries must be in numerical
(or alphabetical) order.
This is generally not true for sets.
- Place commas between the elements
- Your answer should start with a "{" and end with a "}"
Exercise 1
A={1,2,3,4,5,6,7,8,9,10} B={2,4,6,8,10,12,14,16,18,20}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 2
A={1,2,3} B={3,4,5,6}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 3
A={a,b,c,d,e,f,g,h,i,j} B={a,e,g,x,y,z}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 4
A={11,22,33,44,55,66,77,88,99}
B={4,8,12,16,20,24,28,32,36,40,44,48,52,56,60,64,68,72,76,80,84,88,92,96,100}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 5
A={a,e,f,h,k,l,m,n,o,s,u,v,w,y,z} B={b,d,g,i,k,l,o,q,t,u,v,w,z}
Go to the top of this page
Go to the set home page
Go to the next section
SUBSETS
Let A be the set of objects that you own in your home
Let B be the set of objects that you own which are kept on the second floor of your home
Let C be the set of objects that you own which are kept in your bedroom [Note the bedroom is own the second floor]
Let D be the set of objects that you own which are kept in your bedroom nightstand
Now we could say D is contained within C, which in turn is contained within B, which in turn is contained within A.
This is the notion of a subset.
D is said to be a subset of C since it is completely contained within C (another way to think of this is every element of set D is also an element of set C).
C is said to be a subset of B since it is completely contained within B (another way to think of this is every element of set C is also an element of set A).
B is said to be a subset of A since it is completely contained within A (another way to think of this is every element of set D is also an element of set C).
The symbol for subset is Ì.
So D Ì C and C Ì B and B Ì A.
However if even one element of one set is not contained within the other then thy are not subsets.
If A were defined as {1,2,3,4,5} and B as {3,4,5,6} then B would not be a subset of A since
“6” Î B but 6 Ï A.
The symbol for “not a subset” is Ë.
We would write B Ë A.
The notion of subsets is graphically illustrated below
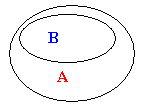
In this first illustration B is entirely within A so B Ì A.
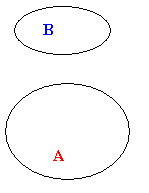
In this second illustration A and B have nothing in common
(A Ç B = {Æ}) so we could write
A Ë B and B Ë A.
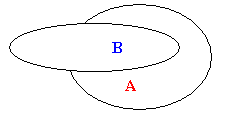
In this last illustration some of B is in A, but not all of B is in A so we could write B Ë A.
Finally we’ll look at two more examples, and then I’ll make one final point
Example 1
A={1,2,3,4,5,6,7} B={2,3,4}
B is entirely within A (i.e. every element of B is also an element of A) so we can write B Ì A
Example 2
A={1,2,3,4,5} B={2,4,6}
Here B Ë A
One last point I need to make then you can work out some examples regarding subsets.
As in the rest of life everything is a matter of perspective.
“A is a subset of B” could also be viewed as “B contains A.”
This notion of "contain" is symbolized by É.
So A Ì B is the same thing as B É A.
In each of the exercises you'll have some sets defined for you, and then there will be
four statements about those sets. Three of the statements will be true, and one of the
statements will be false. Choose the statement that is false.
Exercise 1
A={1,2,3,4,5,6} B={1,2,3} C={3,4,5}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 2
A={1,2,3,4,5,6,7,8,9,10} B={2,4,6,8,10} C={4,8}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 3
A={"red", "blue", "green", "black", "purple"} B={"red" "blue"} C={"black" "brown"}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 4
A={a,b,c,d,e,f} B={a,c,f,h,j} C={a,b,c,d,e,f,h,j}
Go to the next problem
Go to the top of this page
Go to the set home page
Go to the next section
Exercise 5
A={computer files} B={Microsoft Word files} C={Microsoft Excel files}
Go to the top of this page
Go to the set home page
Go to the next section
SET THEOREMS
First of all a "theorem" is a statement that can be proved.
Below are a few theorems involving the concepts of union, intersection and subsets.
Think about them for a while and then go on to the next page for my set wrap-up.
If A Ì B and B Ì C then A Ì C
If A Ì B then A Ç B = A.
If A Ì B then A È B = B.
Go to the top of this page
Go to the set home page
Go to the next page of this unit


