|
|
|
On this page I will be using concepts that were discussed in previous units.
If you are unfamiliar, or unsure of any of these concepts, please take this time
to go back and review them. The concepts used on this page and the links taking you to
their page are listed below:
Let's look at the same examples discussed in that lesson
See! Changing (most) decimals to fractions is easy! Now, you try it!
0.56 = 56/100 = 14/25 (divide both the numerator and denominator by 4)
1.2345
1.2345 = 1 2345/10000 = 1 469/2000.5 = 5/10 = 1/2
Not all decimals are so nice and neat.
Some like 0.3131313131313131313131... repeat the same group of digits infinitely.
Decimals like the one shown are called repeating decimals.
Now believe it or not, this type of decimal can be changed into a fraction with some work
Let's take a look at 0.31313131...
First of all, let's name our decimal n
n=0.313131...
Now, we can see "31" is repeated over and over again
Let's bring one set of "31" out of the decimal by multiplying the decimal by 100
{we need to move the decimal 2 places to the right in order to bring 31 out of the decimal}
100n=31.313131...
Now comes the tricky part
We have two expressions: one about our decimal n and one about 100n.
Let's line up the expressions as shown
100n=31.313131...
n= .313131...
Now if we were to subtract the smaller equation from the larger one, on the left hand side we would have 100n - n which would leave us with 99n
(simply subtract 1 from 100 and leave the n in place),
and on the right hand side we would have 31.313131... - .313131... leaving us with 31.
100n=31.313131...
n= .313131...
99n=31
Now if we divide both sides of our equation by 99 we'll have n=31/99
(On the left hand side 99n/99 = 99/99 * n = 1 * n = n)
But remember n is what we named our continuing decimal, so we finally have a ratio representing the decimal.
All we have to do now is reduce it to lowest terms, and we're finished!
Since 31/99 is in lowest terms already we can conclude
0.31313131... = 31/99
Okay, this is a long process, and it takes some getting used to, so I'll show it to you two more times, then you can practice it yourself
Let's take a look at 0.990990990...
First of all, let's name our decimal n
n=0.990990990...
Now, we can see "990" is repeated over and over again
Let's bring one set of "990" out of the decimal by multiplying the decimal by 1000
{we need to move the decimal 3 places to the right in order to bring 990 out of the decimal}
1000n=990.990990990...
Now comes the tricky part
We have two expressions: one about our decimal n and one about 1000n.
Let's line up the expressions as shown
1000n=990.990990990...
n= 0.990990990...
Now if we were to subtract the smaller equation from the larger one, on the left hand side we would have 1000n - n which would leave us with 999n
(simply subtract 1 from 1000 and leave the n in place),
and on the right hand side we would have 990.990990990... - .990990990... leaving us with 990.
1000n=990.990990990...
n= 0.990990990...
999n=990
Now if we divide both sides of our equation by 999 we'll have n=990/999
(On the left hand side 999n/999 = 999/999 * n = 1 * n = n)
But remember n is what we named our continuing decimal, so we finally have a ratio representing the decimal.
All we have to do now is reduce it to lowest terms, and we're finished!
n = 990/999 = 110/111.
0.31313131... = 110/111
You should be beginning to catch on. For my last trick I intend to something a little more underhanded
Let's take a look at 0.13222...
First of all, let's name our decimal n
n=0.13222...
Now this time we can see that "2" is eventually repeated over and over again,
but before it we have that stubborn "13"
Let's bring the "13" out of the decimal by multiplying by 100
100n=13.222...
Now lets bring one "2" out of the decimal by multiplying by 10
1000n=132.222...
We have two expressions: one about 100n and one about 1000n.
Let's line up the expressions as shown
1000n=132.222...
100n= 13.222...
Now if we were to subtract the smaller equation from the larger one, on the left
hand side we would have 1000n - 100n which would leave us with 900n,
and on the right hand side we would have 132.222... - 13.222... leaving us with 119.
900n=119
Now if we divide both sides of our equation by 900 we'll have n=119/900
0.13222... = 119/900
One last point to make and then you get to play this conversion game.
Isn't it annoying writing the same digit over and over again?
Well some books use a mathematical shorthand for this. A line over the repeating digits.
Using shorthand notation our three problems would look like this:
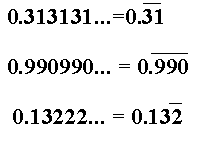
Okay, that's of me rambling on. Now it's your turn to ramble on.
Changing a fraction to a decimal is nothing more than a division problem.
Just divide the numerator by the denominator.
But, you might say "the numeator is smaller than the denominator, how can I divide it?"
That's an excellent question, glad you asked.
The answer is to add a decimal and several zeros to the numerator.
This will be demonstrated in the next example
Chnage 11/16 into a decimal
First of all change this into a division problem
Now write a decimal right above the decimal in 11.0000, and continue as if you were doing whole number division
16 goes into 110 six times. 16 * 6 = 96, and 110-96 = 14
Drop down a zero making the 14 into 140. 16 goes into 140 eight times. 16 * 8 = 128 and 140-128 =12
The division is completed in the next illustration. Verify the last two steps yourself
In each of the following exercises change the fraction into a decimal
To see this in action look no further. The next example is one of a repeating decimal
Change 38/75 into a decimal
First of all write the problem as a division problem. Consider 38 to be 38.00000.
And most importantly place a decimal point directly above the decimal in 38.0000.
Now we'll proceed as though we are doing a whole number division
75 cannot go into 38 so place a "0" above the 8.
75 goes into 380 "5" times. Place a 5 above the "0"
75 * 5 = 375 and 380 - 375 = 5.
Drop a "0" making the 5 into 50.
75 cannot go into 50 so place a "0" next to the "5" in your answer
Drop a "0" making 50 into 500
75 goes into 500 "6" times. Place a "6" next to the "50" in your answer
75 * 6 = 450. 500 - 450 = 50
Repeating the process above drop a zero making 50 into 500
Again 75 goes into 500 "6" times. Place a "6" next to the "506" in your answer
75 * 6 = 450. 500 - 450 = 50
You should by now realize that you are in an infinite loop. You'll keep on making 50 into 500, dividing 75 into 500 "6" times, and coming up with a remainder of 50
place three "..." next to the "5066" indicating that the "6" is being repeated infinitely
Conclusion: 38/75 = 0.5066...